In this problem we find the eigenfunctions and eigenvalues of the differential equation $$\frac{d^2y}{dx^2} + \lambda y = 0$$ on the interval $0\leq x \leq 3$ with boundary values $$y^\prime(0) = 0\hspace{20pt} y(3)+y^\prime(3) = 0$$

For the general solution of the differential equation in the following cases use A and B for your constants, for example $y = A\cos (x) + B\sin(x)$. For the variable $\lambda$ type the word lambda, otherwise treat it as you would any other variable.

Case 1: $\lambda = 0$

(1a.) Ignoring the boundary conditions for a moment, the general solution for the differential equation is

Apply the boundary conditions to the general solution to obtain two equations relating $A$ to $B$:

(1b.) Solving this system for A and B we get
Case 2: $\lambda < 0$

(2a.) Ignoring the boundary conditions for a moment, the general solution is

Apply the boundary conditions to obtain two equations relating $A$ to $B$:

(2b.) If $A$ and $B$ are not both zero then, solving these two equations, one can eliminate both $A$ and $B$ and derive the following formula for $\sqrt{-\lambda}$ in terms of hyperbolic functions ($\cosh, \sinh, \tanh, \coth$, etc.).
(2c.) Choose the graph of $\sqrt{-\lambda}$ and $-\coth\left(3\sqrt{-\lambda}\right)$
A
B
C
D


From the graph there are nonzero eigenvalues for $\lambda$, Sturm-Loiuville guarantees infinitely many eigenvalues, so we go on.

Case 3: $\lambda > 0$

(3a.) Ignoring the boundary conditions, the general solution is

Apply the boundary conditions to obtain two equations relating $A$ to $B$:
(3b.) Assuming $A$ and $B$ are not both zero then, solving these two equations, one can eliminate both $A$ and $B$ and derive the following formula for $\sqrt{\lambda}$ in terms of trigonometric functions.

(3c.) In increasing order, the first four eigenvalues from this equation are:
$\lambda =$
(Your answers should be accurate to at least 7 decimal places.)

List the first three eigenfunctions $y_1(x), y_2(x), y_3(x)$ in order of increasing eigenvalues.
$y_1(x)=$,
$y_2(x)=$,
$y_3(x)=$
Here are graphs of the first four eigenfunctions on $\lbrack 0,3 \rbrack$.

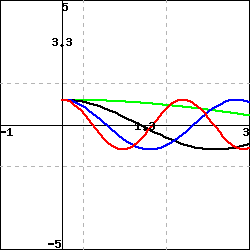
List the functions, ordered by their eigenvalues in increasing order, by their color - green, red, blue, black: