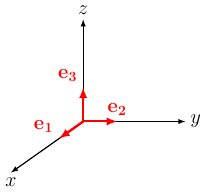
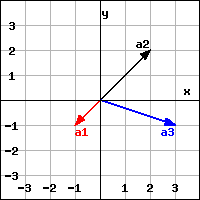
Suppose $f: \mathbb{R}^3 \to \mathbb{R}^2$ is a linear transformation and $f(\mathbf{e_n}) = \mathbf{a_n}$ for $n = 1, 2, 3$.

1. Find a formula for $f$. Your answer should be a coordinate vector with the variables $x$, $y$, and $z$ in its components.
   $f(x,y,z) =$
2. Find the matrix for the linear transformation $f$ (relative to the standard basis in the domain and codomain). That is, find the matrix $A$ such that $f(\mathbf{x}) = A \mathbf{x}$. For instance, enter [ [1,2], [3,4] ] for the matrix ${\left[\begin{array}{cc} 1 &2\cr 3 &4 \end{array}\right]}$.
   $A=$
3. Find the kernel of $f$. Enter your answer as a vector with constant entries, a vector with the variables $x$, $y$, $z$ in its components (using a minimum number of variables), or enter R^3 for $\mathbb{R}^3$.
   $\mathrm{ker}(f) =$
4. Find the image of $f$. Enter your answer as a vector with constant entries, a vector with the variables $x$, $y$, $z$ in its components (using a minimum number of variables), or enter R^2 for $\mathbb{R}^2$.
   $\mathrm{im}(f) =$
5. The linear transformation $f$ is (select all that apply):
   A. injective (one-to-one)
   B. bijective (an isomorphism)
   C. surjective (onto)
   D. none of these