Suppose we are concerned with the function $$f(x) = 2^x.$$ We can evaluate $f$ at natural numbers $x$. Indeed,

$f(1) =$ ,
$f(2) =$ ,
$f(3) =$ ,
$f(4) =$ ,

We are going to approximate $f$ by three polynomials, of degrees 1, 2, and 3. Let's call them $p_1$, $p_2$, and $p_3$, respectively.
$p_1$ will be determined by the requirement that $$p_1(1) = f(1) \quad \hbox{and}\quad p_1(4) = f(4).$$
$p_2$ will be determined by the requirement that $$p_2(1) = f(1), ~p_2(3) = f(3) \quad \hbox{and}\quad p_2(4) = f(4).$$
$p_3$ will be determined by the requirement that $$p_3(1) = f(1), ~p_3(2) = f(2), ~p_3(3) = f(3) \quad \hbox{and}\quad p_3(4) = f(4).$$
Thus $p_1$ is simply the linear function whose graph passes through the points $(1,2)$ and $(4,16)$. In fact,
$p_1(x) =$ . $p_2$ is the quadratic function whose graph intersects the graph of $f$ in the points $(1,2)$, $(3,8)$, and $(4,16)$. $p_3$ is the cubic function whose graph intersects the graph of $f$ in the points $(1,2)$, $(2,4)$, $(3,8)$, and $(4,16)$.
The idea is illustrated in this Figure:
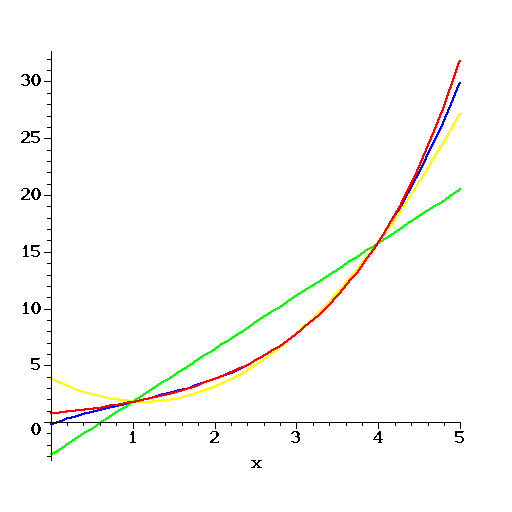
The graph of $f(x) = 2^x$ is shown in red. The graph of $p_1$ is green, that of $p_2$ is yellow, and that of $p_3$ is blue. The blue graph is mostly covered up by the red graph, which indicates how closely the cubic polynomial $p_3$ approximates the exponential $f$, particularly in the interval $[1,4]$.